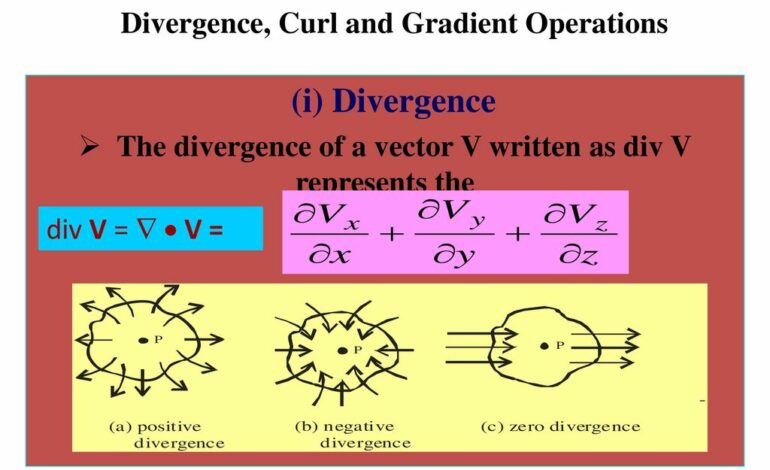
What is the Physical Interpretation of Divergence?
Understanding the concept of divergence is essential for mastering fundamental math, physics, and science equations. Despite seeming daunting, this article provides ample examples and explanations. Divergence refers to changes in physical quantities, such as temperature or pressure, over time and space. By comprehending its physical significance, you can better understand advanced concepts like the divergence theorem and integration theory. This article explores how two simple mathematical expressions can provide extensive knowledge about nature. Let’s begin our journey toward understanding divergence and its importance in various fields of study.
Meaning of Divergence
Divergence is a significant concept that can illuminate the physical implications of equations and mathematical manipulations. Simply put, it measures the degree to which something has spread out from a central point. It can be expressed as a flow of electricity, mass, or energy, indicating how a quantity changes over time and space. This information can help us understand the behavior of air molecules in different locations or energy velocity as it moves through materials. Divergence also helps us comprehend the relationship between different magnitudes within forces, such as the movement of heat from a source. Understanding gradients and directional derivatives is essential to grasp the physical implications of divergence.
What Is Divergence in Physics?
Divergence in physics refers to the measure of how a vector field diverges or converges to a given point. If a field is divergent, particles do not leave the system, creating an imbalance and causing them to move away from each other. Consider how a garden hose works, with water flowing through it and spreading out due to gravity and atmospheric pressure. Conversely, convergent fields ensure that particles coming in will exit, creating an equilibrium and causing particles to move closer together. Vacuum cleaners are an excellent example of convergent fields. These phenomena are critical to understanding how particles interact with each other in the physical world.
Types of Divergence
Regarding the physical significance of divergence, there are two types to consider: gravitational and electromagnetic.
- Gravitational Divergence
- Electromagnetic Divergence
Applications of Divergence
The physical significance of divergence gives it a range of applications. In mathematics, this concept is helpful in fields like thermodynamics, electromagnetism, and fluid dynamics. But the significance goes beyond mathematics: let’s look at some applications.
- Fluid Dynamics
- Electromagnetism
- Weather Predictions
Implications of Divergence
In physics, divergence plays a significant role in understanding the behavior of energy and matter – especially in an electromagnetic field.
When a field has divergence, energy or matter moves or propagates outward from a source, spreading out over the environment, on the other hand, if the field has no divergence, energy or matter is not spreading out and will resemble something more uniform and condensed.
Properties of Divergence
When it comes to divergence, there are three main properties you should be aware of:
- It’s addictive
- It’s directional
- It’s rotational
Conclusion
In summary, divergence is vital to various physical processes in nature and daily life. It plays a significant role in complex equations and helps us comprehend the behavior of waves and heat flow. The physical importance of divergence has been widely researched in thermodynamics, electricity, magnetism, and even fluid dynamics. As a fundamental concept in physics, it helps us comprehend the universe better.







